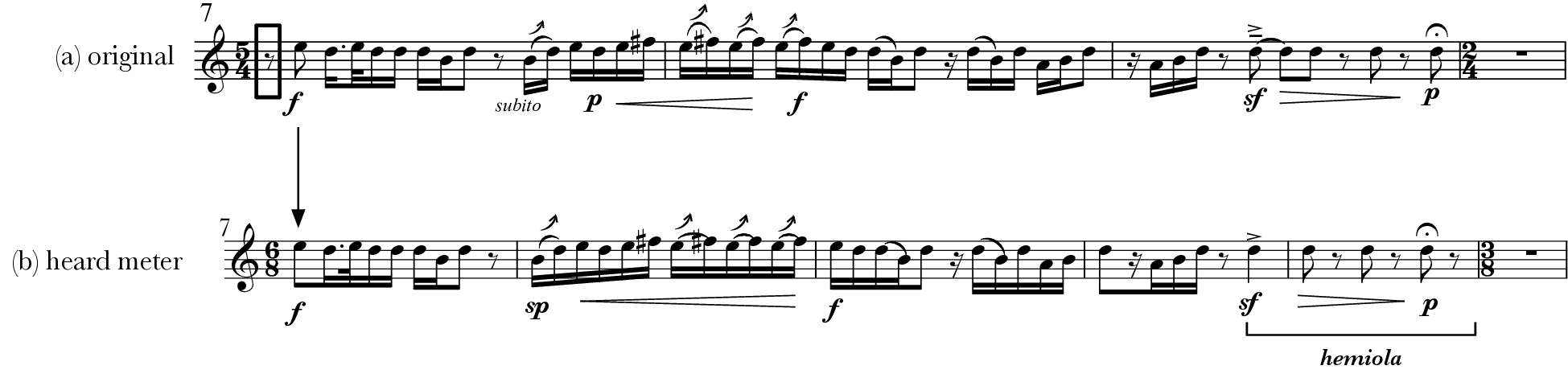Synchronizing Meter with Melody: Metric Organization and Voice Leading in Wang Amao's One Person's Stage

Introduction

This paper explores the perceived metrical organization and its interaction with the overarching linear progression guided by the pentatonic scale in Wang Amao’s One Person’s Stage (2021)—a solo piece for the Chinese two-string bowed instrument called the alto board fiddle. Wang Amao (王阿毛, b. 1986) studied composition with Chen Yi, Zhou Long, James Mobberley, and Paul Rudy at the University of Missouri-Kansas City, where she received both her MA and PhD in composition. She is now Associate Professor of Composition at the Xinhai Conservatory of Music in Guangzhou, China. This piece was commissioned by Hu Yu (胡瑜, b. 1981), Associate Professor of Chinese board fiddle and Associate Dean of the Department of Chinese Music at the Beijing Central Conservatory, who also premiered the same piece on December 10, 2021. A recording of this premiere is available online (Wang Amao [2023]). This paper adheres to the Chinese naming convention, listing surname followed by the given name for the composer and the performer. An earlier version of this paper was presented at the 13th Biennial International Conference on Music Since 1900 in Leuven, Belgium and the 2024 Annual Meeting of the Society for Music Theory in Jacksonville, Florida. I am grateful for the insightful and constructive feedback provided by the reviewers during the development of this research. I also thank Trevor de Clercq and Kyle Hutchinson for their support throughout the writing process. Since the board fiddle may be unfamiliar to Western readers, Example 1a shows the front and back sides of the instrument (a), and the seated posture of playing it (b). The board fiddle (板胡), less known than the popular Chinese violin, the erhu, is noted for its piercing sound quality and ability to simultaneously play two strings, which inspired Wang to explore its auditory potentials. For comparison between the erhu and board fiddle, see Stock (1993, 277–80).

When I first approached this piece, the metrical organization struck me in terms of how it is notated and how it is perceived. To illustrate this point, Example 2 presents two contrasting interpretations of the metrical structure in a phrase (mm. 7–10) from the Introduction: the notated meter printed in the score (a) and the meter I perceive based on the performer Hu Yu’s 2021 recording (b). The recording referenced in this article refers to Wang Amao (2023). Although the composer notates this phrase in a non-isochronous 5/4 meter concluded by a full measure of rest in 2/4, my hearing favors an isochronous 6/8, omitting the initial eighth-note rest in the original score. To investigate the reasons behind this rhythmic divergence, I interviewed both the composer and the performer, gaining insights into how and why this divergence occurs. Example 3 presents a summary of my findings from these interviews. My interviews were conducted over multiple days from September 2023 to June 2024. I will specify each interview date for different quotations.

In our initial conversation on October 7, 2023, Wang explained that her intention, as demonstrated in Example 3(a), is to highlight the core of the melody, manifested in m. 8 and underscored by the only strong downbeat pitch, which is articulated through a local registral and dynamic climax. The remaining subdivisions within the 5/4 measure begin with syncopations, enhancing the rhythmic dynamism. As each subdivision portrays a rolling melodic figure undulating above and below an E₅–D₅-axis, the patterns vary, featuring different combinations of eighth notes and sixteenth notes as well as collections of pentatonic pitches. Pentatonic scales are the primary pitch foundation for traditional Chinese art and folk musics. Many Chinese composers of the twentieth and twenty-first centuries continue to embrace pentatonicism in their works. For a general survey of pentatonic usage, see Antokoletz (2014, 466–75). For a more focused examination of the integration between pentatonicism and serialism, see Rao (2002). During a separate conversation on June 24, 2024, Wang further connected her motivic and metrical design to the Daoist “must-change” principle and the meaning of her work’s title. She stated:

“Varied thematic and motivic iterations, combined with constant changes in the uneven 3+2 metrical subdivisions, embody the Daoist philosophy of ‘infinite changes’ (千變萬化). While similar motivic cells interact with uneven metric subdivisions and syncopations, I can flexibly extend or condense the length of a melodic cell, rendering the phrase rhythm more spontaneous and more unpredictable. This mirrors the state of continuous change, akin to a person stumbling a few repetitive yet varied words in an unrehearsed monologue on stage—hence, I have named my work One Person’s Stage.” For related discussion on infinite changes, see Wang, “Philosophizing Time in Sinitic Opera” (2023).

Wang’s statement provides clear notational details, emphasizing each melodic cell and its placement within a rhythmic matrix gridded by non-isochronous meter and syncopation. The succession of these constantly changing melodic cells delineates an overall imagery gesturing toward continuous rhythmic instability, akin to what Wang describes as the “spontaneity” and “unpredictability” of stage improvisation. Contrasting with this sense of improvisation, my interview with Hu reveals a different understanding of the phrase structure as presented in Example 3(b.1).

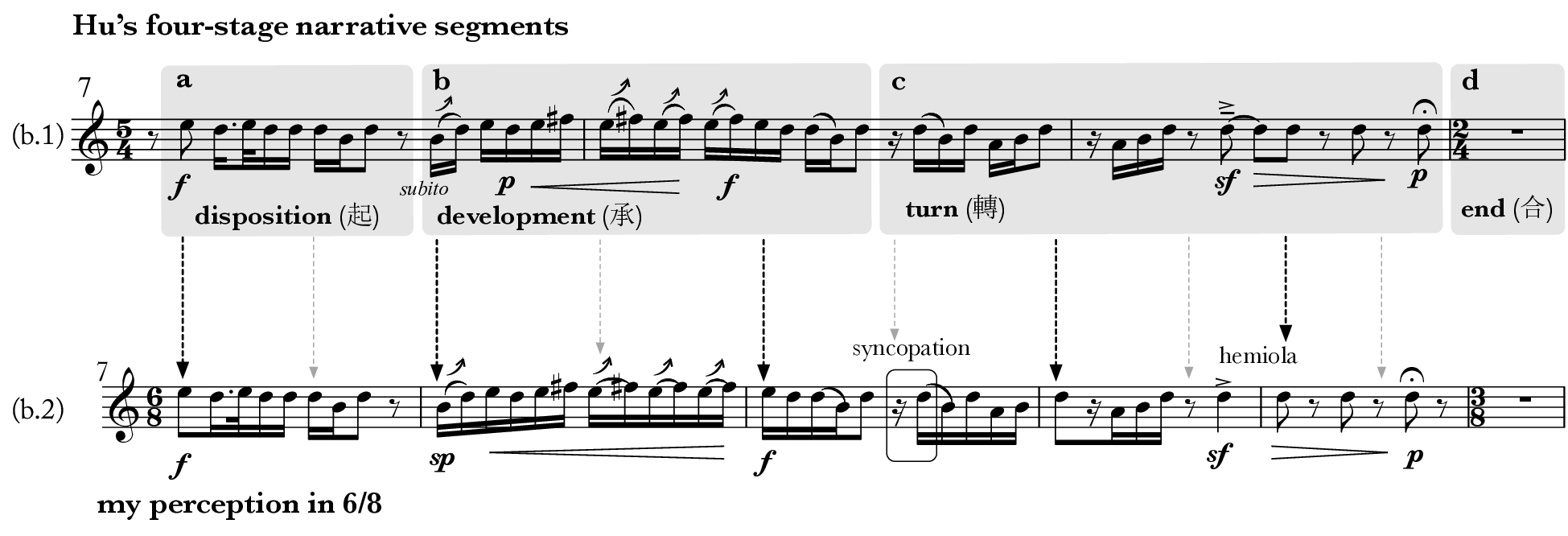
Departing from Wang’s focus on smaller melodic units, Hu divides the phrase into four larger melodic segments, a–d. The first three segments exhibit distinct yet interconnected motivic patterns, each progressively expanding in length from 1 to 1.5 to 2.5 measures. His explanation, given on September 8, 2023, reads:

“In teaching and learning Chinese instruments and singing, we always draw parallels between phrase rhythm and the four-stage development used in classical Chinese literary writing for unfolding a narrative. This can be best explained through a four-line Tang-poem, where each line depicts a particular function in terms of the narrative positioning—disposition (起), development (承), turn (轉), and end (合). I borrow the English translation for these four stages in Nancy Yunhwa Rao’s 2020 article, where she examines the influence of Tang poetry narrative techniques on musical structure and momentum in Chen Yi’s chamber work Happy Rain on a Spring Night. Mastering the phrase rhythm through this four-stage unfolding is essential for understanding the natural ebb and flow of a phrase from its start to close. This method has long been ingrained in my practice, and I also apply the same approach to partition this phrase into four segments, with my performance interpretation articulating the rhythmic flow of my segmentations.”

Since these melodic segments correspond to various stages of narrative unfolding, I call them narrative segments. Hu then elaborates on the unique characteristics of these four segments and their interconnectedness. This paragraph summarizes my notes taken during our conversation on the same date. The opening, disposition (a), introduces the thematic and motivic idea, featuring rolling figures undulating between a major second (E₅⟷D₅) and a minor third (D₅⟷B₄). The development phase (b) enlivens the theme with sliding notes, short slurs, and a crescendo. Its pitch contour portrays a more elastic shape delineated by extensive sequence of the motivic rolling figures. The turn (c) varies the rhythmic and intervallic motives by introducing a new melodic leap of a perfect fourth (D₅⟷A₄), syncopation, and hemiola, adding angularity and thus signaling change. The whole-measure rest in the final segment (d) extends the atmosphere of tranquility continued from the soft dynamics and a sustained fermata at the close of the third segment. This enables the music to gently dissipate, serving as the last part (end) of the entire phrase. Interestingly, during the 2024 SMT Annual Meeting (November 9, 2024), Philip Stoecker and Matthew Arndt enthusiastically shared with me that they perceive this phrase as more closely aligned with a Western sentential structure, where disposition establishes presentation, development suggests continuation, and turn and end together create closure.

After Hu described his phrase partitioning, I was struck by how seamlessly his narrative segments aligned with my metrical perception when reinterpreted within a 6/8 framework, as represented by the arrows connecting Examples 3(b.1) to 3(b.2). Enthusiastic about this discovery, I shared with him my understanding of the underlying metric flow as I experienced it while listening to his performance. I then showed him how various musical markings—such as dynamic variation, slides, slurs, and pitch apexes—accentuated the perceived 6/8 downbeats. The reader can go online to experience this 6/8 interpretation (Wang Amao [2023], 0:37–0:52). Hu acknowledged that although he had not been fully conscious of it, he had indeed been entraining to a 6/8 meter throughout.

We are now faced with two contrasting metrical readings: one from the composer and the other informed by my listening experience that aligns with Hu’s interpretation of the formal process. Although Wang’s intent is to evoke improvisatory-like rhythms, my perception reveals underlying metrical regularities. These regularities emerge through the clearly articulated alternation of strong and weak beats that pulse through different stages of the narrative segments. While Wang’s original compositional intent remains significant and warrants further exploration, this study prioritizes the perceptual aspects of the music as it unfolds in the listener’s ear, specifically in the Introduction of One Person’s Stage (mm. 1–28).

Additionally, this paper engages the perceived meter alongside voice leading guided by the pentatonic E-shang mode scale {E, F♯, A, B, D}—the first rotation of the pentatonic collection on D—through different sections of the Introduction. The reader can go ahead first to Example 7(b) for the construction of the pentatonic E-shang mode, derived from the pentatonic collection on D. Like Western diatonic modal structures, the pentatonic scale can generate five distinct modes through successive rotations: gong mode (宮調式, original position), shang mode (商調式, first rotation), jue mode (角調式, second rotation), zhi mode (徵調式, third rotation), and yu mode (羽調式, fourth rotation). For details on Chinese modal theory, see Ho and Han (1982, 133–35). Example 4 illustrates the tonic E being prolonged from the start of the music and continuing through the first two-thirds of Part . By closely observing the interactions among the perceived meters, the pentatonic pitch collection, and the formal structure, I consider how these elements converge to create a cohesive musical narrative. I begin by explaining the tripartite formal scheme of the Introduction and then proceed to demonstrate my approaches to the heard meter and prolongational voice leading, while also considering whether the four-stage narrative method can be consistently applied to explain the natural growth and decline of other parts of the form.

Analysis

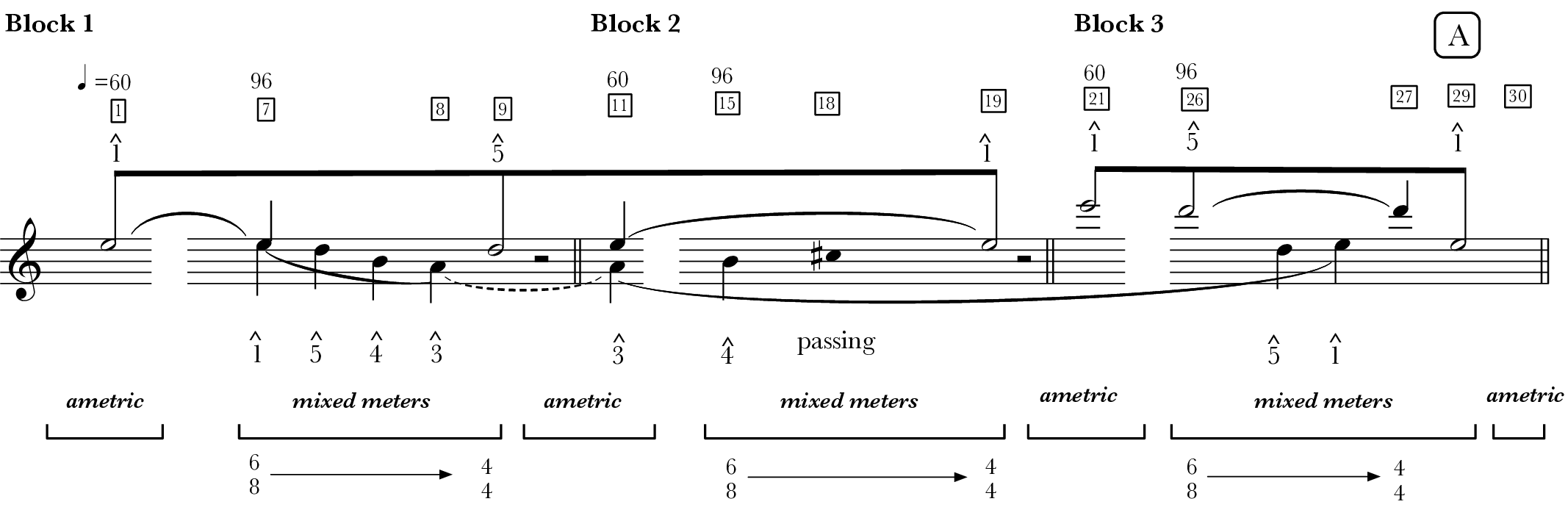
Example 5 presents three distinct blocks—demarcated by half rests in m. 10 and m. 20—showcasing significant structural parallelisms. Each block is internally divided into two juxtaposed sections defined by contrasting tempo and texture. Whereas the initial section is marked as 60 BPM, the subsequent section accelerates to 96 BPM. I use tempo to define each section: slow and fast. In the slow section, the texture unfolds two interwoven layers, where an unhurried, calm melody is supported by a sustained voice either from above or below. In the fast section, the texture thins out to a single rolling, fluid melody driven by a motoric rhythm. The driving force is then halted, as articulated by a long rest (blocks 1 and 2) or a long-held note (block 3); the closure of block 3 then overlaps with the beginning of the next formal part .

According to Hu, he applies the four-stage narrative unfolding to interpret both slow and fast melodies in all three blocks. Previously, Example 3(b.1) walked the reader through the four-stage construction of the fast melody from block 1; here in Example 5, I will use the slow melody from the same block (mm. 1–6) to demonstrate the formation of the four narrative segments, A–D. Below is Hu’s explanation of how segments A–D are derived:

“The disposition (A) introduces a single pitch E₅ on the upper string. The development (B) slightly enlivens this pitch by repeating it on the lower string. Notice how the long-held note on this string is created by different tied rhythms, which influence my bowing technique. In the turning stage (C), the music starts to incorporate more melodic elements, using pentatonic intervals of major seconds and minor thirds. Finally, m. 6 softly presents an octave E₅–E₆ on both strings, bringing a peaceful ending to the entire phrase” (April 4, 2024).

Thus, both slow and fast melodies in block 1 adhere to the four-stage narrative structure, and Hu continues to partition the remaining phrases from blocks 2 and 3 based on their varied reiterations of the thematic/motivic materials from segments A–D (in the slow melody) and a–d (in the fast melody). Most recently, Sullivan (2024b) explores how performers shape the listening experience in passages of motive-driven metric manipulation in post-tonal music. Reading Example 5 synchronically, the narrative segments are aligned in a way that highlights the thematic parallels across different formal blocks: capital letters represent segments from the slow sections, while lowercase letters represent those from the fast sections. Horlacher (2011) also examines how varied iterations of a melody sectionalize different formal blocks in Stravinsky’s works from his Russian and Neo-Classic periods. My alignments of the narrative segments in Example 5 draws inspiration from Horlacher’s graphical representations. In the slow sections, segments {A, A´, A´´} launch with a long-held, quiet E₅ (or E₆); {B, B´, B´´} begin to introduce rhythmic activity; Pitch-wise, the B₅–A₅ (m. 12) and F♯₅–A₅ (m. 13) in B´ are motivically derived from the descending major second and ascending minor third in segment C (mm. 3–4). Rhythmically, however, Hu defines mm. 12–13 as the development segment B´ because it follows A´ and initiates minor rhythmic activities, similar to the situation in segment B, block 1. {C, C´, C´´} vary the rhythm and timbre; Such as different dynamic markings in C/C´ or tremolos in C´´. and {D, D´, D´´} return to a long sustained note marked by a decrescendo. In the fast sections, segments {a, a´, a´´} begin forte with pitch emphasis on D₅ (or D₆); {b, b´, b´´} present a sequence of rolling sixteenth notes articulated by slurs and sliding notes; {c, c´, c´´} inject a rocky, angular feeling with large melodic leaps and fragmented rhythmic figures (c and c´) or ostinati (c´´); and {d, d´, d´´} present a sense of calm with full-measure rests or long-sustained notes.

The narrative segments in Example 5 illuminate how each melody increases and decreases its motion in terms of rhythmic and dynamic arrangements. During my interview with Hu on the same date (April 4, 2024), I further inquired about the application of the four-stage narrative structure within a larger formal context. His response resonates with the Daoist philosophy pointed out by Wang at the beginning of this paper. He explained:

“I believe the essential element here relates to the ideological Daoist principle of ‘infinite changes.’ This concept sheds light on the relentless, varying interactions among all worldly phenomena, thereby nurturing boundless possibilities for creative thought. In the four-stage narrative, each stage represents a change that interacts with its adjacent stages, producing a sonic imagery abundant with sounds of continuous change. If we apply this ‘constant changing state’ to the overall tripartite formal scheme of the entire Introduction, we hear three blocks unfold a continuous change in tempo, texture, number of concurrent lines, dynamics, elaborations, and articulations. This is how I rehearse and interpret the entirety of One Person’s Stage—constant changes within each and among the three blocks.”

Hu’s insights illuminate the nuanced interplay between the internal variations within each phrase and how they are built into a constantly evolving global narrative over the course of the entire Introduction. In my analysis, I use my perception of meter as a means of exploring how these internal changes interact with the overarching narrative by altering the sense of metrical pulse in different segments and sections of the form.

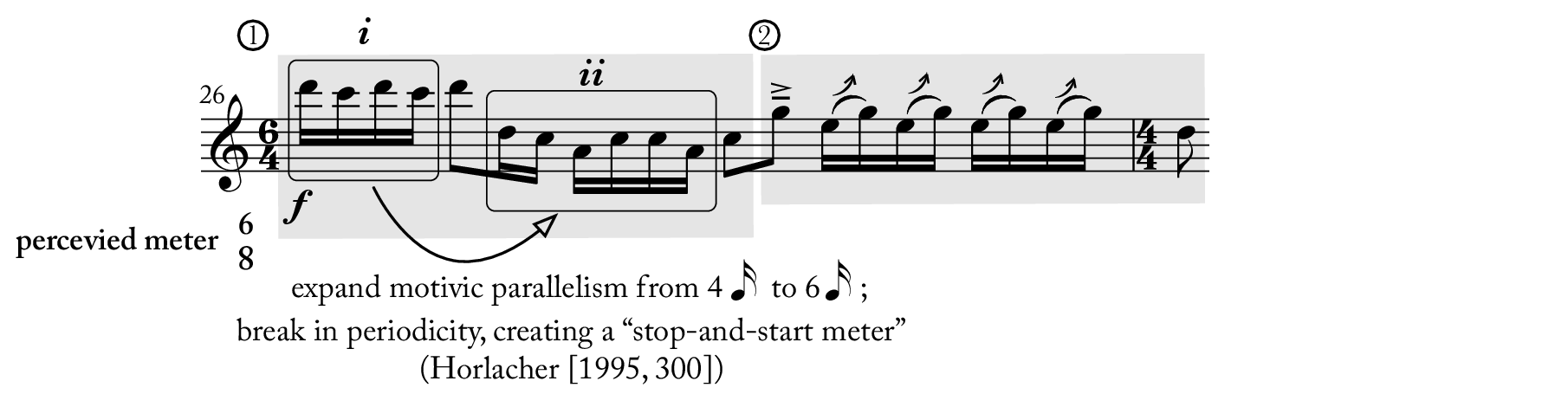
While my re-barring in Example 3(b.2) allows for straightforward metric reinterpretation, other phrases might challenge this method. For instance, how do we rebar the slow sections, where the local metric pulses are erratic, with temporary, unconnected, and irregular rhythmic fragments? Also, in the fast sections from blocks 2 (mm. 15–20) and 3 (mm. 26–29), some places break metric periodicity and disrupt a simple, consistent re-barring approach. In Example 6, for instance, the two grey boxes mark off fragments and ① and ②, each counted in 6/8. A challenge arises, however, in addressing the motivic expansion from four sixteenth notes (unit i) to six sixteenth notes (unit ii) in ①, breaking the otherwise continuous metric periodicity. This motivic expansion is achieved through ambiguity of pitch parallelism. Initially, D₅–C₅ in unit ii partially repeats D₆–C₆–D₆–C₆ in i. However, the following four sixteenth notes (A₄–C₅–C₅–A₄) invite another interpretation, relating the rolling minor thirds in ii to the rolling major seconds in i. Regardless of the interpretation adopted for the motivic expansion, the extra eighth-note pulse in ii interrupts the rhythmic regularity in 6/8 and postpones the appearance of the concluding eighth-note on C₅. This requires a pause in the metrical counting at the end of ① and a reset on the next emphatically punctuated G₅ in ②, creating what Gretchen Horlacher might term a “stop-and-start” meter. Horlacher (1995, 300). To accommodate these issues, I incorporate James Sullivan’s methodology (2023), which develops the concepts of projection theory (after Mirka [2009]) and metrical categorizations. Sullivan’s approach offers greater metrical flexibility, making it suitable for examining both the lack of clear meter in the slow sections and the disrupted metrical periodicity—or metrical reset—in the fast sections. I will first explain projection theory along with my metric analysis of block 1 in Example 7(a), reserving the metrical categorizations for a more detailed investigation of the same block later.

To understand the metric sketches presented in this and the subsequent examples, it is necessary to first explain the notational details. The circle dots placed below the staves represent the foreground metrical pulses as defined by Sullivan, while the square ones underneath the fast section indicate hypermetrical groupings (after Lerdahl and Jackendoff [1983]). Brackets above each staff illustrate the three types of Sullivan’s metrical categories. Pitches highlighted by grey rectangles in the fast section draw out a complete pentatonic scale. The open-top square ⎵ in segments c denotes the metrical disruption, shifting from a dotted quarter pulse to a quarter note pulse. This notation is adapted from Horlacher’s example (1995, 299).

In narrative segment a (m. 7), A₁ and A₂ stand for the initial attacks. The timespan between them () acts as a hypothesis for the location of the third A₃. Since this hypothesis is fulfilled, the projected timespan is then confirmed (), serving as the basis for further projected arrows () and generating the beats/pulses (notated by circle dots). If the hypothesis is unfulfilled and A₃ does not occur on time (as “?” in mm. 3–5, segment C), the projection fails, and beats are not generated. The unfulfilled hypothesis corresponds to the first kind of Sullivan’s ametricity: unconfirmed projections. This establishes the “three-attack threshold” policy on the lower level, where the three evenly and regularly spaced attacks, A₁–A₂–A₃, function as note onsets cueing the meter. The dots are only felt as beats once A₃ confirms the projection, and the ensuing projections can extend further only if there are convincing attacks to support them. The projections can occasionally “withstand some absent attacks but not persist indefinitely” (Sullivan 2023, [3.7]). Sullivan also claims that the absent attacks can include rests (2023, [4.3]). For instance, narrative segment c (m. 8) opens with a sixteenth rest. Yet, this brief silence does not fundamentally alter the established eight-note pulse from preceding segments a and b. Instead, the eighth-note pulse continues through this short pause to the subsequent on-beat attacks in the remainder of segment c. Additionally, I argue that this sixteenth rest, along with the resulting syncopated effect, accentuates a second strong beat within the 6/8 context, presenting a stark contrast to segments a and b, where every dot aligns with an actual attack. The projections vanish once the music enters segment d, where the full-measure rest consistently suppresses any audible attacks.

There is a temporal limit constraint for forming a projection: 0.2–2.0 seconds for the lower level (i.e., between A₁ and A₂) and 5.0–6.0 seconds for the higher (between A₁ and A₃). Any timespan falling outside of this range is challenging to perceive and thus ametric, making it unqualified to launch a proper metric process. In segments A and B, for instance, the long-held notes under the tempo marking of quarter note equals 60 sustain well beyond the 2.0 second upper limit. Such wide timespan intervals prevent initiating projections. Conversely, the thirty-second note in B is too short to form a projection, with timespan of only 0.125 seconds, which is below the lower limit of 0.2 seconds. Thus, it does not induce any hypothesis with regard to the meters. Both long-held notes and the succinct thirty-second note are classified into Sullivan’s second kind of ametricity: uninitiated projections.

Based on metrical preference rules, as defined by Lerdahl and Jackendoff (1983, 74–96), Mirka (2009, 39), based on various forms of accents and changes in music, further classifies the rules into six different types that influence metric perception: subjective, phenomenal, structural, grouping, streaming, and parallelism. The groupings discussed in this paper correspond to her subjective category (e.g., strong beat early), phenomenal category (e.g., dynamic and durational stress), and parallelism category (e.g., thematic parallelisms). we can group several attacks at the unit level to form a temporary perception of 6/8 meter from m. 7 to the beginning of m. 9. These rules include phenomenal accents, preference for an early strong beat in a group, and motivic parallelisms. The phenomenal accents consist of strong downbeats articulated by dynamic stress, durational stress, and the beginning of slur-slide figures. The last item requires clarification on how the combination of slurs and slides forms a phenomenal accent. When playing slurs and slides simultaneously (particularly the first pair in the sequence of repeated figures in m. 8), Hu explained that he uses a blend of increased bow pressure and speed at the start, with the left hand adding an additional accent (June 24, 2024). Thus, the dynamics and intensity at the beginning of the slur-slide figure are more pronounced, drawing the listener’s attention to the start.

Regarding the second preference rule, observe the relationship between the perceived 6/8 meter and the narrative segments: the accentuated downbeats are placed at the beginning of each of the segments a, b, and c. The change of narrative segments thus aligns with the preference rule for an early strong beat in a group. The third rule, thematic parallelisms, describes how the parallel narrative segments from the fast melodies across the blocks, such as a/a´ or b/b´/b´´, share identical or similar metric structures owing to the repetition of motivic and rhythmic figures. (We will revisit this rule more fully in Examples 8 and 9 below).

We can now examine Example 7(a) in more detail, including Sullivan’s three types of metrical categorizations. The names of these types are placed above each musical staff. The opening slow section—the ametric—evokes a feeling of stasis (mm. 1–5), owing to both the uninitiated projection at the start as well as several unconfirmed projections oscillating between F♯₅ and C♯₅ around the sustained E₅ in the lower string. As this section concludes, the sense of rhythmic flow slowly rises (in m. 6), moving in a dotted-quarter-note pulse. While the music transitions to the fast section, the beat fluctuates to an eighth note, with the phenomenal accents (dynamics and slur/slide figures) in segments a and b promoting a strong, consistent, 6/8 count. A change in the 6/8-count is triggered once the melody enters in segment c—the turning stage. This change manifests itself through the emergence of more vibrant rhythmic activities, most notably the onset of the second strong beat within a performed 6/8 measure, the syncopated rhythm at the start, and the mixed meter at the end (where the 6/8 stops, and a new quarter-note pulse arises, giving way to the 4/4 meter). Following Sullivan’s system, the quarter-note level is indicated with solid arrows, as it has been subconsciously elaborated in the preceding measures and now surfaces for the first time. The whole rest in segment d continues the serenity produced by the decrescendo at the end of segment c, producing a tranquil ending that echoes the calm, ametric opening of this section.

The sustained regularity in the active portion of the melody gives rise to a sense of hypermeter, which is reinforced by the dynamics. My hypermetric groupings, utilizing Lerdahl and Jackendoff’s dotted notation (1983; represented as squares), disclose a continuous strong-weak pattern across the four narrative segments. The hypermetrically articulated pitches in the fast melody, marked by grey rectangles, along with the maximum and minimum pitches, form a complete pentatonic scale: the E-shang mode (E 商調式), the construction of which will be explained in the following paragraph. I adapt and modify Schenkerian theory to sketch the pentatonic texture centered on E, and further investigate the interplay between deep prolongational voice leading and metrical stream.

Example 7(b) presents the first rotation of pentatonic scale on D, resembling Western diatonic modal structures where scales, in various rotation, outline different modes. The resultant scale, represented by the open noteheads, is referred to as the pentatonic E-shang mode. This scale is characterized by an intervallic pattern alternating between major seconds and minor thirds. The original non-rotated form is called the pentatonic D-gong mode (D 宮調式). For constructions on various Chinese modal pentatonic forms, review footnote no. 10. I use five consecutive scale degrees,  to , to label each note, thereby reinforcing both the pentatonic center on E and the structural hierarchy of the five notes. In addition to the pentatonic pitches, Wang incorporates chromatic notes in the Introduction, which I mark with filled-in noteheads to distinguish them from the underlying pentatonic gamut. The chromaticism consistently fills the scale-steps that are a minor third apart: between ⟷ and ⟷. To incorporate these four foreign notes in my scale-degree system, I label them as ♯, ♭, ♯, and ♭ to denote the nearest semitonal relationship to their respective pentatonic scale degrees. It is crucial to emphasize that the ♯ and ♭ signs used for scale-degrees are intended to conceptually highlight the strong semitonal relationship linking the chromatic pitches to their closest pentatonic scale-degrees. They abstractly correspond to the accidentals of the actual pitches as notated in the score.

While adopting Schenkerian analysis to a pentatonic context could warrant a separate article, this analysis primarily focuses on how the tonic, E, is prolonged by scale-step motion along these five consecutive pentatonic scale degrees. The scale-step motion in this context includes the adjacent scale-degrees that are a major second (⟷, ⟷, and ⟷) or a minor third apart (⟷ and ⟷). My approach deviates from prior Schenkerian analyses of unaccompanied melodies, such as J. S. Bach’s Cello Suites analyzed by Karl-Otto Plum (1988) and Christopher Parks (2006), which does not account for traditional functional musics that prolong triads. Instead, my sketches capture the main linear features observed in Wang’s Introduction, explaining the voice-leading prolongation in her music without generalizing the approach to pentatonic works by other contemporary Chinese composers. The presence of pitch ornamentations, whether from within or outside the scale collection, indicates a deeper prolongational layer. The ornamentations encompass stepwise motion (passing notes, [in]complete and double neighbors, and linear progressions), leaps (arpeggiations and couplings), or both in combination (unfoldings). They stratify the overall texture into two layers: a primary voice sustaining  supported by a subordinate voice portraying motion into an inner voice via various linear progressions.

Example 7(c) presents my sketches. Initially, the slow section stays on E₅ over the first five measures. The momentary appearances of F♯₅ (m. 3 and m. 5) and C♯₅ (m. 4) function as elaborations, with the former serving as a pentatonic neighbor tone and the latter as a chromatic arpeggiation. They do not fundamentally distract from the focused hearing of this long, silky sustention on . Toward the end of this section (m. 6),  comes to the fore with a noticeable crescendo to mp followed by a significant pull to the registral climax of E₆ on the lower string. Although the two strings are played simultaneously, the slow section delineates a monophonic texture, wherein a coupling links two different registers on  elaborated by an upper neighbor. Conversely, the single fast melody projects a polyphonic texture fabricated by two distinct, contrapuntal voices. The primary (top) voice continues the motion from the slow section, prolonging the E tonic. It traces a linear descent from  to  decorated by an upper neighbor. The subordinate voice portrays a stream moving from the established  into an inner voice via a descending 4-line progression that reaches the pitch minimum in this phrase ().

Having now gathered information on voice-leading and meter, we can explore their interaction, as shown in Example 7(d). The primary voice, composed of up-stemmed pitches and stretching the entirety of block 1, becomes rhythmically enlivened near the end of the first turning segment (C, m. 6); an upper neighbor not only elaborates the long-sustaining tonic E but also triggers regular beats that transform the preceding ametricity into metrical motion, propelling the melody forward. The rhythmic vitality intensifies as it extends into the fast section. In response to this intensification, I revisit and adjust some voice-leading pitches to foster a closer interaction with more prominent (hyper)metrical articulation. These adjusted pitches are shaded in the fast section to highlight their alignment with the rhythmic structure. While my earlier selection of voice-leading pitches in the fast section largely considered their initial appearances in the music as structurally significant and their repetitions as part of a prolongational process, the repositioning of some pitches to more metrically articulated locations ensures that the voice leading, when interacting with the metric structure, aligns more closely with my perception.

The two instances of  and the penultimate  in the primary voice are now hypermetrically stressed, distributed across three successive narrative segments: a, b, and c. The upper neighbor, repositioned near a local accent at the intermediate level, is less metrically stressed, consistent with its function as an elaboration. Similarly, in the subordinate voice, the rhythmically adjusted  and  align with weaker yet still prominent beats:  on the unit level and  on the hypermeteric level. Alongside the final , which is the only note without beat support, the pitches in the subordinate voice alternate with those that are strongly stressed in the primary voice, gently pulsing through the lower range of register within the metric hierarchy. This example highlights the fact that the voice-leading structure is a product of meter, where the former emphasizes structurally significant pitches and the latter accentuates their rhythmic placement in different formal sections and segments. The evident interplay between voice leading, meter, and narrative segments continues into the next two blocks, and I will use a more integrated prose in what follows to discuss the relationships between pitch, meter, and form.

The metric organization in block 2 (Example 8a) mirrors that of block 1, juxtaposing two mixed meters bookended by an ametric fragment. In the slow section, the crescendo towards a forceful forte progressively increases the energy imparted to the strings, driving them into more vigorous motion. Despite the dynamic intensity, this section only rhythmically engenders a few sporadic uninitiated and unconfirmed projections, hardly affecting any sense of meter. The start of a new narrative unfolding process in the fast section simultaneously conjures up a 6/8 pulse. The recognition of segment a´ as a melodic parallel to segment a in block 1 enables the perception of meter to surface sooner than the three-attack threshold. It preserves the rhythms and pitch content of segment a with variations in melodic contour. Therefore, I use solid arrows to signal the 6/8 pulse at the start of the fast section. While the music progresses to b´, it develops its preceding parallel segment b by introducing a metrical reset owing to two apparent factors. First, the intrusion of the dotted rhythm distinctively signals the onset of the metrical accent. Second, this dotted rhythm occurs on a C♯ foreign to the pentatonic E-shang mode. This chromaticism creates a sense of markedness within a pentatonic context, thereby highlighting the distinctive rhythmic activity and leading to the perception of a metrical reset at both local and hypermetrical levels. The other three hypermetrically strong beats are emphasized by either strong dynamics (m. 15 and m. 19) or the breakdown of the B–D motivic parallelism (m. 16). The 6/8 shifts once more in the subsequent turning segment, c´, where the syncopations reshape the metric grouping from dotted quarter to quarter, altering the preceding 6/8 narrative to a temporary 4/4.

Example 8(b) charts the voice leading in this passage. The voice-leading notes are drawn from those shaded pitches in Example 8(a). The stable quality of the open fifth in the slow section is upheld by a long-lasting ametric temporality, sustaining the static nature of this perfect interval. As the meter is awakened in segments a´ and b´ and the rhythms become more animated, pulsing in a quick 6/8 time, the pitches also form a pair of unfoldings that connect the preceding open fifth to produce two distinct moving voices. The lower, subordinate voice presents an ascending 3-line progression, ⟶  ⟶ ♭, where  and ♭ are both hypermetrically stressed after passing the formal border from the slow to the fast section. The upper main voice sustains the tonic E₅, first via a lower neighbor and then via an ascending 3-line progression,  ⟶  ⟶ ♭, that reaches to the registral climax. These elaborations fill the gap between adjacent hypermetrical beats, bridging the space from one strong beat to the immediately following weak beat. They then fade into the rhythmic background, as most of them do not receive any metric accentuation. The concluding  in the main voice (c´) is the last pitch metrically emphasized. It occurs precisely at the point where the 6/8 meter stops and a new 4/4 begins.

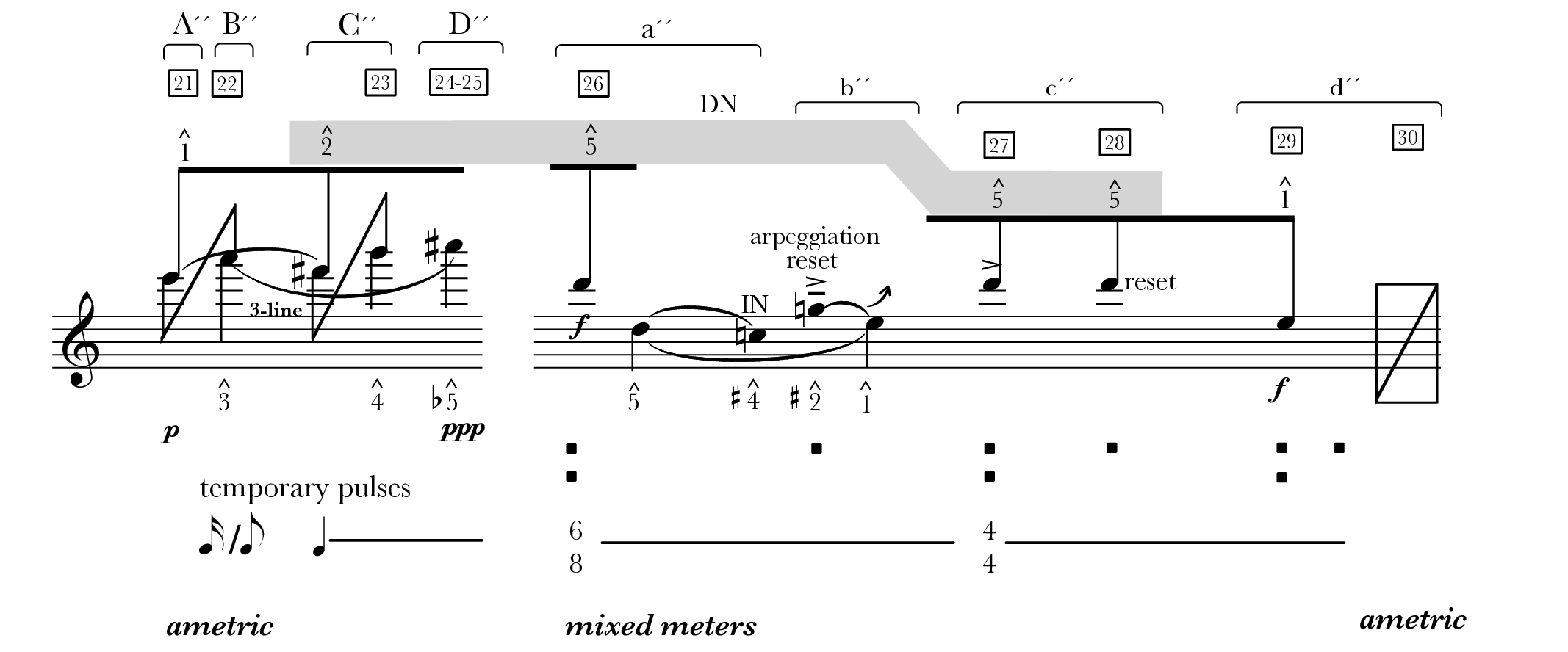
Although the slow section in block 3, shown in Example 9a, is globally ametric, it differs from the previous two blocks by containing several ambiguous local projective regularities in segments B´´ and C´´, which creates a subtle hint of pulsation travelling fluidly through the ametrical space. Segment B´´ articulates low-level hierarchies of sixteenth- and eighth-note pulses that quickly dissipate into the long-held dotted half note before segment B´´ ends. I must clarify that I treat these projections as if the performance were strictly in time, because Hu puts so much rubato that it adds a level of fluidity and irregularity, which obscure the projections. They may delineate the first kind of Sullivan’s ameter (the unconfirmed), where attacks are spaced unevenly and do not confirm the initial hypothesis. I appreciate one of the reviewers for pointing this out to me. Thus, this analysis reveals an underlying structure with potential regularity, offering insights into the score-based hearing. Segment C´´ initially becomes more metric and fluctuates to quarter notes. However, the long whole-note tremolos challenge our ability to perceive whether the quarter-note beats can maintain their regularity within the rapid alternation between F♯₆ and B₆. While I certainly hear an intrinsic regularity produced by the consistent alternation between notes, their rapidness also simultaneously disrupts the clarity of the quarter-note beat. An ambiguity thus arises whereby the metric regularity is intertwined with metric obscurity: I use grey arrows to portray such ambiguous projections. This tension remains active until the beginning of segment D´´, where an exceedingly long and subdued rest relaxes the tension and reinforces the global ametricity in this section.

The disruptions to metrical periodicity continue into the fast section, including local resets and a shift in meter from 6/8 to 4/4. Based on melodic parallelism, I also use solid arrows to indicate the 6/8 at the beginning of segment a´´. This segment repeats the melodic and intervallic components of descending major seconds and ascending minor thirds, while omitting the initial eighth-note and dotted-note pattern present in the original segment a. These disruptions not only infuse angularity to the otherwise flowing rhythm but also signal changes in narrative segments (reset in b´´ and 4/4 in c´´). Thus, there is a growing sense of metrical irregularity across the fast sections in the three blocks. Whereas block 1 contains only the meter change (m. 9), block 2 introduces the metrical reset (m. 16) while maintaining the meter shift (m. 17). Block 3 contains the greatest extent of abruptness, with the resets and meter change alternating throughout the fast melody.

Example 9(b) illustrates the interaction between pitch and metric organization. The passage spans a wide registral range from octave designations 7 to 5, where the voice leading consistently fluctuates between coupling and maintaining the primary register. These wide registral leaps add an additional layer of angularity to an already ragged rhythmic texture. The primary voice prolongs , embellished by double neighbors of  and . Similar to the previous two blocks, the voice leading here connects pitches that are mostly hypermetrically stressed in the fast section. In the slow section, the subordinate voice gently recapitulates the 3-line progression of ⟶♭ from block 2, but in an exceptionally high register above the primary voice. In the fast section, segments a´´ and b´´ strive to draw the motion back to the primary register, depicting the movement from the lower neighbor  to . This attempt is elaborated by the chromatic ♯ and ♯. The effort, however, ultimately recedes into the rhythmic background, with only ♯ weakly punctuated on the higher metrical level. The pulling of the lower neighbor  (m. 27) back to the register of D₆ in segment c´´ further contributes to this receding effect, emphasizing the shift by moving to a new 4/4 meter stressed by strong beat. All of these efforts attempting to reconcile the motion between different octave registers ultimately find resolution in segment d´´, where  settles in the true register of E₅ articulated by the last pair of strong-weak beats.

Example 10 summarizes the background voice-leading sketches and metrical organization for the entirety of the Introduction, revealing three formal attributes worthy of further discussion. First, linking the subordinate voice across the three blocks yields an overarching symmetrical down/up 4-line progression that traverses from  to  and back to . This voice is mostly active in the three fast sections, with pitches moving along the E-shang mode scale-steps and pulsing through the 6/8. Second, the main voice repeats a lower neighboring motion that prolongs . The first –– spans the initial two blocks and stays within the primary register, while the second covers block 3, linking the primary register with higher octaves. The rhythm in the main voice features more varied metric structures, with pitches either sustained in long and static temporality in the slow sections or occurring at or near the point where meter shifts at the end of the fast sections. Third, although the three blocks are separated by long rests, they are—from the perspective of Sullivan’s metrical categorical type—seamlessly connected through a sense of ametricity. The long rest concluding each block is followed by unimitated or unconfirmed projections at the start of the next block. Combined with these unestablished projections, the extended pause contributes minimally to a consistent rhythmic momentum between the blocks, thus blurring the formal boundaries.

Conclusion

This paper has explored the relationship between the perceived metric organization and the voice-leading structure, drawing on Hu’s formal interpretation of the four-stage narrative unfolding process. To conclude, I revisit the composer’s original intentions regarding “unpredictability” and “spontaneity,” linking them with my analysis to demonstrate how my aural experience aligns with Wang’s compositional design.

As a listener, the moments that best evoke unpredictability and spontaneity are found in the temporary metric projections within the slow sections, rather than in the fast melody suggested by Wang at the outset of my paper (Example 3(a)). While the consistent alternation of strong-weak beat groupings in the fast melody limits my perception of spontaneity and unpredictability, the fleeting, momentary metric projections in the slow sections evoke a far stronger sense of fragmentary and unexpected rhythmic events. I focus on one specific moment—the slow section from block 3 (Example 11)—to illustrate my points.

As discussed earlier, this section contains two subtle pulsations that flow fluidly through the texture. Fragment 1 introduces a sudden, transient sixteenth-note projection, creating a brief sense of rhythmic regularity that quickly dissipates into a long-held dotted half note. Fragment 2 follows, attempting to reestablish a pulse, but now with a different quarter-note beat. As this quarter-note pulse unfolds, however, its identity becomes increasingly obscured by tremolos that blur the clarity of the beat. Just as I begin to perceive the pulse, it again dissolves into an extended held note, leaving the fragment unresolved.

These sudden projections—emerging briefly only to vanish—convey a strong sense of metrical unpredictability and spontaneity. Additionally, Sullivan (2024a) extends his concept of moment-to-moment rhythmic structure by drawing parallels to the meter of poetic texts, which he describes as “rhyme-oriented reading” (338) or “poetic phenomenal accents” (340). For me, they evoke the impression of someone narrating a story onstage without a script. The narrator begins by offering a few words (fragment 1) but abruptly halts, leaving the thought incomplete. Then, unsure how to proceed, they introduce new words (fragment 2, represented by the dashed curve and arrow). As they attempt to continue, they falter, timidly repeating the new words (fragment 2, the grey arrows) before ultimately leaving the idea without conclusion. This interpretation, while grounded in my metric analysis, provides a complementary perspective on the composer’s intended spontaneity and unpredictability in One Person’s Stage. It highlights how these fragmented rhythmic gestures reflect performative uncertainty, aligning with the composer’s vision of a musical narrative that embraces fleeting, unplanned moments.

Works Cited

• Antokoletz, Elliot. 2014. A History of Twentieth-Century Music in a Theoretic-Analytical Context. New York: Routledge.

• Ho, Lu-Ting and Han Kuo-Huang. 1982. “On Chinese Scales and National Modes.” Asian Music 14 (1): 132–54.

• Horlacher, Gretchen. 1995. “Metric Irregularities in ‘Les Noces’: The Problem of Periodicity.” Journal of Music Theory 29 (1): 285–309.

• Horlacher, Gretchen. 2011. Building Blocks: Repetition and Continuity in the Music of Stravinsky. Oxford: Oxford University Press.

• Lerdahl, Fred, and Ray Jackendoff. 1983. A Generative Theory of Tonal Music. Cambridge, MA: MIT Press.

• Mirka, Danuta. 2009. Metric Manipulations in Haydn and Mozart: Chamber Music for String, 1787–91. Oxford: Oxford University Press.

• Park, Christopher. 2006. “E♭ and its Extra-Musical Meaning to Two Bach Cello Suites.” In Essays from the Fourth International Schenker Symposium, Vol. 1, edited by Allen Cadwallader, 65–84. Hildesheim: Georg Olms Verlag.

• Plum, Karl-Otto. 1988. “Towards a Methodology of Schenkerian Analysis.” Translated and edited by William Drabkin. Music Analysis 7 (2): 143–64.

• Rao, Nancy Yunhwa. 2002. “Hearing Pentatonicism through Serialism: Integrating Different Traditions in Chinese Contemporary Music.” Perspectives of New Music 40 (2): 190–231.

• Rao, Nancy Yunhwa. 2020. “The Concept of Shi: Chinese Aesthetics and Happy Rain on a Spring Night (2004).” Music Theory Online 26 (3).

• Stock, Jonathan P. J. 1993. “An Ethnomusicological Perspective on Musical Style, with Reference to Music for Chinese Two-Stringed Fiddles.” Journal of the Royal Musical Association 118 (2): 276–99.

• Sullivan, James. 2023. “Extending the Parallel Multiple-Analysis Processor: Perceived Meter in Post-Tonal Music.” Music Theory Online 29 (4).

• Sullivan, James. 2024a. “Review of Lines and Lyrics: An Introduction to Poetry and Song, by Matt BaileyShea (Yale University Press, 2021).” Music Theory Spectrum 46 (2): 333–42.

• Sullivan, James. 2024b. “Performing Meter: Toward A Motive-Oriented Performance Practice For Post-Tonal Music.” Music Theory Online 30 (4).

• Wang, Amao. 王阿毛. 2023. “One Person’s Stage.” Banhu: Hu Yu. Soundcloud Recording. https://soundcloud.com/wangamao/hgqcnkhgfqdy?si=bf46a545675e46d3873fad8dbad8c64b&utm_source=clipboard&utm_medium=text&utm_campaign=social_sharing.

• Wang, Anna Yu. 2023. “Philosophizing Time in Sinitic Opera.” Music Theory Online 29 (3).